近日，信息科学与工程学院付鑫婕副教授作为第一作者，在期刊Chaos, Solitons & Fractals在线发表了题为“Non-periodic intermittent stochastic control for SVIQR epidemic model on complex network with saturation incidence rate”的研究论文。
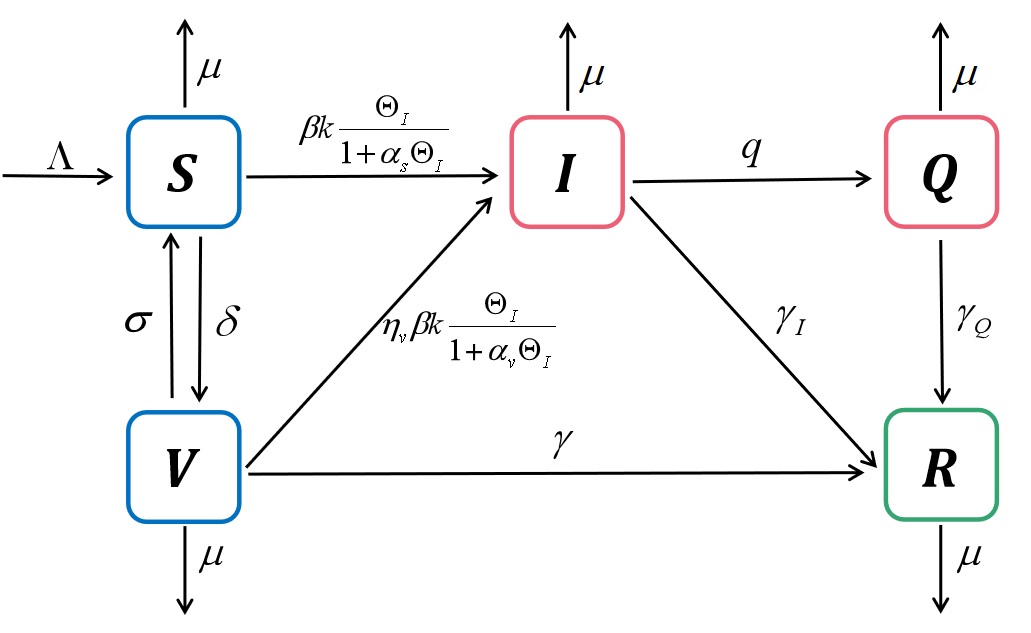
该研究针对易感个体与感染个体有效接触数达到饱和的现实情况，建立了基于复杂网络并采用饱和发生率的SVIQR传染病模型（流程图如下）。研究中成功计算了模型的基本再生数，并严格证明了无病平衡点与地方病平衡点的全局渐近稳定性。考虑到疫苗接种后免疫失效带来的传播不确定性，为有效控制疫情，研究创造性地设计了一种由G-布朗运动驱动的非周期性间歇性随机控制策略（示意图如下）。运用切比雪夫不等式和伊藤公式等随机理论工具，研究建立了模型几乎必然稳定的理论条件。
此外，研究采用LHS-PRCC法对关键参数进行了敏感性分析，并通过数值模拟验证了理论结果的有效性（部分模拟结果图如下）。数值模拟清晰显示，与单一随机控制策略相比，当模型同时引入g-型扰动和h-型扰动时，网络中的感染节点平均密度显著降低，并提前收敛至0，有效抑制了传染病的传播。
论文链接：https://www.sciencedirect.com/science/article/abs/pii/S0960077925006848。
编 辑：万 千
审 核：贾 波
鲁公网安备 37090202000305号